Peter Müller
Globewide Network Academy (GNA)
pmueller@uu-gna.mit.edu
The previous sections already introduce some ``object-oriented'' concepts. However, they were applied in an procedural environment or in a verbal manner. In this section we investigate these concepts in more detail and give them names as used in existing object-oriented programming languages.
The last section introduces abstract data types (ADTs) as an abstract view to define properties of a set of entities. Object-oriented programming languages must allow to implement these types. Consequently, once an ADT is implemented we have a particular representation of it available.
Consider again the ADT Integer. Programming languages such as Pascal, C, Modula-2 and others already offer an implementation for it. Sometimes it is called int or integer. Once you've created a variable of this type you can use its provided operations. For example, you can add two integers:
int i, j, k; /* Define three integers */ i = 1; /* Assign 1 to integer i */ j = 2; /* Assign 2 to integer j */ k = i + j; /* Assign the sum of i and j to k */
Let's play with the above code fragment and outline the relationship to the ADT Integer. The first line defines three instances i, j and k of type Integer. Consequently, for each instance the special operation constructor should be called. In our example, this is internally done by the compiler. The compiler reserves memory to hold the value of an integer and ``binds'' the corresponding name to it. If you refer to i you actually refer to this memory area which was ``constructed'' by the definition of i. Optionally, compilers might choose to initialize the memory, for example, they might set it to 0 (zero).
The next line
i = 1;
sets the value of i to be 1. Therefore we can describe this line with help of the ADT notation as follows:
Perform operation set with argument 1 on the Integer instance
i. This is written as follows: i.set(1).
We now have a representation at two levels. The first level is the ADT level
where we express everything what is done to an instance of this ADT by the
invocation of
defined operations. At this level, pre- and postconditions are used to
describe what actually happens. In the following example, these conditions are
enclosed in curly brackets.
{ Precondition: i = n where n is any Integer }
i.set(1)
{ Postcondition: i = 1 }
Don't forget that we currently talk about the ADT level! Consequently, the
conditions are mathematical conditions.
The second level is the implementation level, where an actual representation is chosen for the operation. In C the equal sign ``='' implements the set() operation. However, in Pascal the following representation was chosen:
i := 1;
In either case, the ADT operation set is implemented.
Let's stress these levels a little bit further and have a look to the line
k = i + j;
Obviously, ``+'' was chosen to implement the add operation. We could read the part ``i + j'' as ``add the value of j to the value of i'', thus at the ADT level this results in
{ Precondition: Let i = n1 and j = n2 with n1,
n2 particular Integers }
i.add(j)
{ Postcondition: i = n1 and j = n2 }
The postcondition ensures that i and j do not change their values.
Please recall the specification of add. It says that a new Integer
is created of which the value is the sum. Consequently, we must provide a
mechanism to access this new instance. We do this with the set operation
applied on instance k:
{ Precondition: Let k = n where n is any Integer }
k.set(i.add(j))
{ Postcondition: k = i + j }
As you can see, some programming languages choose a representation which
almost equals the mathematical formulation used in the pre- and
postconditions. This makes it sometimes difficult to not mix up both levels.
A class is an actual representation of an ADT. It therefore provides implementation details for the used data structure and operations. We play with the ADT Integer and design our own class for it:
class Integer {
attributes:
int i
methods:
setValue(int n)
Integer addValue(Integer j)
}
In the example above as well as in examples which follow we use a notation which is not programming language specific. In this notation class {...} denotes the definition of a class. Enclosed in the curly brackets are two sections attributes: and methods: which define the implementation of the data structure and operations of the corresponding ADT. Again we distinguish the two levels with different terms: At the implementation level we speak of ``attributes'' which are elements of the data structure at the ADT level. The same applies to ``methods'' which are the implementation of the ADT operations.
In
our example, the data structure consists of only one element: a signed
sequence of digits. The corresponding attribute is an ordinary integer of a
programming language![]() . We only define two methods setValue()
and addValue() representing the two operations set and add.
. We only define two methods setValue()
and addValue() representing the two operations set and add.
Definition (Class) A class is the implementation of an abstract data type (ADT). It defines attributes and methods which implement the data structure and operations of the ADT, respectively. Instances of classes are called objects. Consequently, classes define properties and behaviour of sets of objects.
Recall the employee example of chapter 3. We have talked of instances of abstract employees. These instances are actual ``examples'' of an abstract employee, hence, they contain actual values to represent a particular employee. We call these instances objects.
Objects are uniquely identifiable by a name. Therefore you could have two distinguishable objects with the same set of values. This is similar to ``traditional'' programming languages where you could have, say two integers i and j both of which equal to ``2''. Please notice the use of ``i'' and ``j'' in the last sentence to name the two integers. We refer to the set of values at a particular time as the state of the object.
Definition (Object) An object is an instance of a class. It can be uniquely identified by its name and it defines a state which is represented by the values of its attributes at a particular time.
The state of the object changes according to the methods which are applied to it. We refer to these possible sequence of state changes as the behaviour of the object:
Definition (Behaviour) The behaviour of an object is defined by the set of methods which can be applied on it.
We now have two main concepts of object-orientation introduced, class and object. Object-oriented programming is therefore the implementation of abstract data types or, in more simple words, the writing of classes. At runtime instances of these classes, the objects, achieve the goal of the program by changing their states. Consequently, you can think of your running program as a collection of objects. The question arises of how these objects interact? We therefore introduce the concept of a message in the next section.
A running program is a pool of objects where objects are created, destroyed and interacting. This interacting is based on messages which are sent from one object to another asking the recipient to apply a method on itself. To give you an understanding of this communication, let's come back to the class Integer presented in section 4.2. In our pseudo programming language we could create new objects and invoke methods on them. For example, we could use
Integer i; /* Define a new integer object */ i.setValue(1); /* Set its value to 1 */
to express the fact, that the integer object i should set its value to 1. This is the message ``Apply method setValue with argument 1 on yourself.'' sent to object i. We notate the sending of a message with ``.''. This notation is also used in C++; other object-oriented languages might use other notations, for example ``->''.
Sending a message asking an object to apply a method is similar to a procedure call in ``traditional'' programming languages. However, in object-orientation there is a view of autonomous objects which communicate with each other by exchanging messages. Objects react when they receive messages by applying methods on themselves. They also may deny the execution of a method, for example if the calling object is not allowed to execute the requested method.
In our example, the message and the method which should be applied once the message is received have the same name: We send ``setValue with argument 1'' to object i which applies ``setValue(1)''.
Definition (Message) A message is a request to an object to
invoke one of its methods. A
message therefore contains
Consequently, invocation of a method is just a reaction caused by receipt of a message. This is only possible, if the method is actually known to the object.
Definition (Method) A method is associated with a class. An object invokes a method as a reaction to receipt of a message.
To view a program as a collection of interacting objects is a fundamental principle in object-oriented programming. Objects in this collection react upon receipt of messages, changing their state according to invocation of methods which might cause other messages sent to other objects. This is illustrated in Figure 4.1.
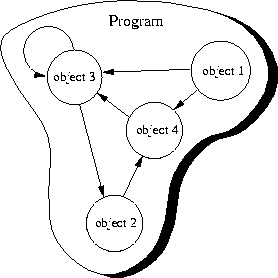
Figure 4.1: A program consisting of four objects.
In this figure, the program consists of only four objects. These objects send messages to each other, as indicated by the arrowed lines. Note that the third object sends itself a message.
How does this view help us developing software? To answer this question let's recall how we have developed software for procedural programming languages. The first step was to divide the problem into smaller manageable pieces. Typically these pieces were oriented to the procedures which were taken place to solve the problem, rather than the involved data.
As an example consider your computer. Especially, how a character appears on the screen when you type a key. In a procedural environment you write down the several steps necessary to bring a character on the screen:
You do not distinguish entities with well-defined properties and well-known behaviour. In an object-oriented environment you would distinguish the interacting objects key and screen. Once a key receive a message that it should change its state to be pressed, its corresponding object sends a message to the screen object. This message requests the screen object to display the associated key value.